Update: I've finally (nearly two years later) created a dedicated GitHub repo for this.

Inspired by this Stack Overflow question, I started thinking about possible ways of implementing the IList<T> interface in a lock-free concurrent data structure, with the following notes:

1. I highly doubt a lock-free Insert or RemoveAt implementation is possible. I could be wrong, of course; but I don't think so. So I would implement those explicitly (and throw a NotSupportedException).
2. I would want guaranteed O(1) random access, at least. (Otherwise, the whole point of implementing IList<T> seems kind of questionable.)

OK, so, how do we do it?

Before I even describe my idea (still a work in progress), I should disclose the fact that, to my simultaneous disappointment and delight, it appears I managed to come up with a concept on my own that is remarkably similar to what researchers at Texas A&M University, including Bjarne Stroustrup, designed and published.

Here's the basic idea. Clearly utilizing a single array that is resized on certain Add operations would be problematic: allocating a new array and copying all elements to it in a lock-free way would be, at least I have to speculate, quite costly (imagine multiple concurrent threads all copying elements concurrently—seems very wasteful). So I considered using a linked list of arrays, where when an Add call requires additional storage, a new array could be allocated and appended to the linked list. But once you introduce a linked list, random access in O(1) becomes, well, less possible.

I was thinking you probably couldn't do it with a simple array of arrays (e.g., a List<T[]>) simply because then you'd eventually run into the problem of having to resize the "outer" array eventually. But then it dawned on me: assuming Count is bounded at int.MaxValue, we could actually use a fixed-size array of arrays.

If each array is twice the size of the previous one, this means we'd only need an array big enough to reach a total capacity of int.MaxValue, which ends up being a measly 32 (quite reasonable for a concurrent data structure, if you ask me)!

This is assuming the first array has a Length of 1. How do I figure? Believe it or not, I didn't have to do any fancy math. The answer is actually quite simple when you visualize array sizes as binary numbers.

That is, if the first array's Length is 1, then its size is:

00000000000000000000000000000001

Then, if the second array's Length is 2 (twice the previous), then its size is:

00000000000000000000000000000010

And, of course, 1 + 2 = 3, or:

00000000000000000000000000000011

Now, if the next array's Length is 4 (again, twice the previous), then that's:

00000000000000000000000000000100

And 4 + 3 (the capacity of the previous two arrays) = 7, or:

00000000000000000000000000000111

See a pattern?

So the first six elements (just for illustration) of this "outer" array would look like this:

The beauty of this design is that it facilitates O(1) random access, when you consider the following: the starting "index" of each array is the sum of the lengths of all previous arrays, which is in turn the sum of a geometric sequence:

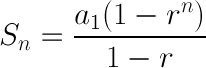
Determining which array a particular index falls into, then, requires simply rearranging the above formula to solve for n:

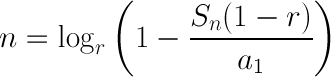
With an a₁ of 1 and an r of 2, this translates to the following code:

int GetArrayIndex(int index)
{
    double n = Math.Log(index + 1, 2);
    return (int)Math.Truncate(n);
}

Pretty simple, right?

Believe it or not, the main issue I've encountered so far is having an accurate O(1) Count operation. To understand why, consider this implementation of Add:

public void Add(T element)
{
    int index = Interlocked.Increment(ref m_index) - 1;

    int arrayIndex = GetArrayIndex(index);
    if (arrayIndex > 0)
    {
        index -= ((int)Math.Pow(2, arrayIndex) - 1);
    }

    if (m_array[arrayIndex] == null)
    {
        int previousArrayLength = m_array[arrayIndex - 1].Length;
        Interlocked.CompareExchange(ref m_array[arrayIndex], new T[previousArrayLength * 2], null);
    }

    m_array[arrayIndex][index] = element;

    Interlocked.Increment(ref m_count);
}

Notice anything fishy? The call to Interlocked.Increment(ref m_index) happens before element is inserted into the array, which means using m_index as Count will result in "false positives," by which I mean values higher than the actual number of elements inserted. However, the "workaround" in the above implementation—maintaining a separate m_count field and calling Interlocked.Increment(ref m_count) at the end of the Add method—also has a flaw: if two Add operations take place concurrently, m_count may be incremented after the higher index first, resulting in the following problem:

for (int i = 0; i < list.Count; ++i)
{
    // This element may not have been set yet!
    T element = list[i];
}

This is something I haven't worked out 100% yet. The structure designed by Stroustrup et al. resolves this issue by utilizing a Descriptor object which describes the most recent operation performed on the array and is updated with a single CAS (compare-and-swap) instruction. What I don't like about this is that it means every call to Add allocates a new object. A small one, yes, but an object nonetheless.

Personally, I like the idea of a ConcurrentList<T> class that allows thread-safe appends, O(1) random acccess, and does not produce (much) garbage. What I have so far seems to meet these requirements, while exhibiting some "iffy" behavior surrounding the Count property.

And honestly, I'm wondering if that's OK; maybe we can just embrace eventual consistency and say this implementation is efficient and just has a "fuzzy" Count.

Anyway, like I said, it's still a work in progress. But once I've gotten it to a state that I like (with unit tests, etc.), I will push it to my GitHub repo!

Try not to get too excited ;)